Start with examples

If you’ve ever read about the programming language Haskell, it’s likely you encountered some explanation of an abstract structure called a monad. If so, it’s almost as likely you’ve encountered the line “a monad is just a monoid in the category of endofunctors”, which is nonsense to everyone but category theorists. It’s often repeated humorously, but it’s also a prime example of a terrible yet common way to explain a new concept. I myself have read or watched many “simple introductions” to monads that started far too abstractly to be of any help to the uninitiated.

Try to recall a lecture or lesson (it’s often in math) where you were lost when a concept was first introduced, but eventually it clicked for you. For me, I’ve noticed the clicking usually doesn’t occur until we start discussing concrete examples. Nonetheless, lessons often start with an abstract concept and then bring in concrete examples to illustrate as they go.

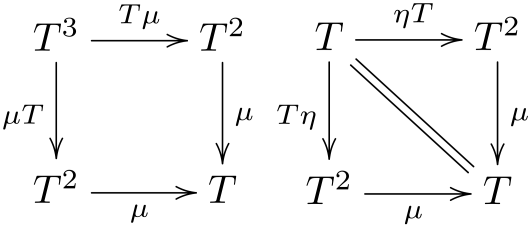
Where does this bias towards the abstract come from? Well, the benefit of abstraction is that it lets us do more reasoning with less thinking. A good abstract concept covers many examples at once, so once you understand it, you can use it to think about things on a higher level more easily. So from the expert’s point of view, explanations wrapped up in abstractions are a more elegant and satisfying way of communicating key insights. “A monad is just a monoid in the category of endofunctors” is succinct and technically contains all the information one needs to grasp monads, so it’s a great explanation if you already know what monoids, categories, and endofunctors are.

So proceeding from the abstract to the concrete works great for experts, but for those learning, I propose that concrete to abstract is the better route. I’ve noticed that the best teachers I’ve learned from do this already. Whenever I am teaching or explaining, I try to think of a good example to start things off. It’s actually a real challenge to come up with a strong example that will make sense to the learner and frame the new concept well, but the right example will have serious payoff in ease of comprehension.

Is there anything you find yourself regularly teaching or explaining? Do you tend to start with examples or abstractions? If you start with examples, what examples do you use and how effective do you think they are? Let me know your thoughts at my Ctrl-C email: gome ​@ ​ctrl-c.club.