Total page count: 866 pages
[2016-05-16] I put together a small photo setup for taking shots of string figures. It is still a work in progress, but will be helpful in making a shots of figures. Eventually I'll put together an album of the figures that I know. The setup consists of putting my laptop on my desk chair, with a dark shirt over the back of the chair for a backdrop. The lamp points towards the black backdrop and lights up the figure. The lighting is a bit too strong and the photos come out overexposed.
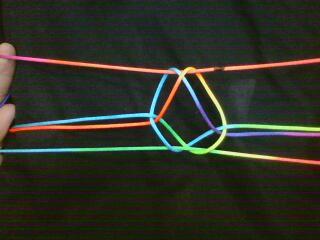
[2016-06-11] The figure below is a slight reworking of the Bolivian figure Footprint from SFM March 2002. The presentation of the Storer code together with the water colouring painting of the final figure is appealing. The colouring of the figure is supposed to mimic the effect of a tie dye string. One can trace through the crossings easily because of the colour.
[2017-11-27]
There is a lot of informaition on the Hex Theory Page.
It is really amazing!
The Zermelo-von Neumann Theorem
The Nash-Hein Ramsey Theorem
The Topological Lemma (both cannot win)
Anatole Beck
The Central Opening Conjecture (Hayward? Jack van Rijswijck? Berge?)
The Nash-Gale Theorem
Ea Ea
Topological Dimension Theory
Oded Schramm
[2017-03-04] At long last, the first batch of percolation criticality numbers are in!
# one hundred trials on a 7x7 board with coin-toss colouring
:! python HexMonteCarlo.py
[[ 1. 3. 4. 4. 5. 8. 5.]
[ 1. 0. 7. 7. 10. 7. 7.]
[ 4. 6. 4. 10. 10. 12. 7.]
[ 4. 6. 9. 9. 4. 8. 8.]
[ 3. 12. 12. 12. 8. 6. 2.]
[ 4. 9. 7. 7. 9. 5. 4.]
[ 15. 6. 5. 5. 5. 0. 2.]]
# ten thousand trials on a 7x7 board
Simulating 7x7 with N=10000 trials
[[ 128. 232. 363. 478. 582. 704. 1065.]
[ 236. 500. 624. 846. 1001. 1077. 806.]
[ 358. 637. 899. 1076. 1120. 982. 554.]
[ 471. 817. 1114. 1165. 1064. 806. 466.]
[ 572. 1028. 1081. 1086. 908. 636. 350.]
[ 767. 1005. 990. 833. 605. 424. 250.]
[ 1014. 751. 555. 448. 323. 226. 116.]]
This shows that percolation criticality follows the main diagonal. It is minimized in the acute corners of the board (A. Beck)
Observe that percolation criticality is connected with "draws". If x is critical then x=1 is a Player 1 win and x=2 is Player 2 win. Thus, the position is a "draw" unless we know the value of x.
[2017-11-11]
The code for the simulator is now available here
[2017-11-27]
Simulator can see when the first player has won.
Given board position:
[[ 0. 1. 0. 0. 0.]
[ 0. 1. 0. 0. 0.]
[ 0. 1. 1. 0. 0.]
[ 0. 1. 0. 0. 0.]
[ 0. 1. 0. 0. 0.]]
Simulating 5x5 with N=500 trials using bernoulli sampling
[[ 500. 0. 500. 500. 500.]
[ 500. 0. 500. 500. 500.]
[ 500. 0. 0. 500. 500.]
[ 500. 0. 500. 500. 500.]
[ 500. 0. 500. 500. 500.]]
Simulator can see when the second player has won.
Given board position:
[[ 0. 0. 0. 0. 0.]
[ 2. 2. 2. 2. 2.]
[ 0. 0. 1. 0. 0.]
[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]]
Simulating 5x5 with N=500 trials using bernoulli sampling
[[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]]
Yay! -- The simulator can see a necessary move. The board template has Player 2 with an almost complete crossing.
Given the board position:
[[ 0. 0. 0. 0. 0.]
[ 2. 2. 0. 2. 2.]
[ 0. 0. 1. 0. 0.]
[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]]
Simulating 5x5 with N=500 trials using bernoulli sampling
[[ 139. 138. 182. 184. 147.]
[ 0. 0. 277. 0. 0.]
[ 154. 138. 0. 170. 156.]
[ 168. 146. 178. 156. 135.]
[ 150. 162. 143. 137. 169.]]
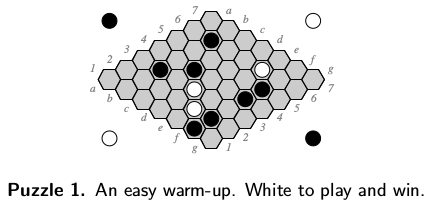
The simulator can solve Hayward Puzzle 1 Note: This puzzle requires a large number (N~10000) trials to solve. Lower numbers of trials tend give incorrect solutions. Notice that tere are several cells close the P(win|x=1) maximizer: [4, 3, 4415.0]
4390. 4314.
4415. 4146.
Given board position:
[[ 0. 0. 0. 0. 0. 2. 0.]
[ 0. 0. 0. 0. 1. 2. 0.]
[ 0. 2. 0. 1. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 2. 0.]
[ 0. 0. 2. 0. 0. 2. 0.]
[ 0. 2. 0. 0. 1. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0.]]
Simulating 7x7 with N=10000 trials using bernoulli sampling
The P(win|x=1) maximizer:[4, 3, 4415.0]
[[ 3397. 3495. 3506. 3817. 4330. 0. 3595.]
[ 3590. 3494. 3666. 3741. 0. 0. 3622.]
[ 3561. 0. 3773. 0. 3827. 3560. 3627.]
[ 3514. 3597. 3588. 4390. 4314. 0. 3554.]
[ 3587. 3642. 0. 4415. 4146. 0. 3613.]
[ 3930. 0. 3568. 3802. 0. 3527. 3492.]
[ 4038. 3434. 3516. 3590. 3617. 3580. 3396.]]
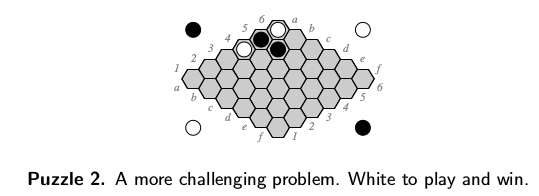
The simulator can solve Hayward Puzzle 2
Given board position:
[[ 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0.]
[ 1. 0. 0. 0. 0. 0.]
[ 2. 2. 0. 0. 0. 0.]
[ 1. 0. 0. 0. 0. 0.]]
Simulating 6x6 with N=10000 trials using bernoulli sampling
The P(win|x=1) maximizer:[4, 2, 4758.0]
[[ 3830. 3884. 3833. 4054. 4151. 4390.]
[ 3847. 3846. 4083. 4290. 4460. 4235.]
[ 3854. 3921. 4203. 4496. 4523. 4137.]
[ 0. 3882. 4493. 4628. 4441. 4154.]
[ 0. 0. 4758. 4406. 4189. 4002.]
[ 0. 4120. 4296. 4069. 3952. 3850.]]
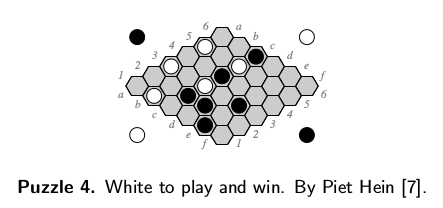
The simulator can solve Hayward Puzzle 4
Given board position:
[[ 0. 1. 0. 0. 0. 0.]
[ 0. 0. 2. 2. 2. 0.]
[ 1. 0. 1. 0. 2. 0.]
[ 0. 0. 2. 0. 0. 0.]
[ 1. 0. 1. 0. 0. 0.]
[ 0. 0. 2. 0. 0. 0.]]
Simulating 6x6 with N=10000 trials using bernoulli sampling
The P(win|x=1) maximizer:[3, 0, 5694.0]
[[ 3925. 0. 3989. 3927. 3927. 4400.]
[ 5060. 4949. 0. 0. 0. 4341.]
[ 0. 4745. 0. 4212. 0. 4351.]
[ 5694. 4394. 0. 4323. 4283. 4119.]
[ 0. 4572. 0. 4259. 4218. 4073.]
[ 5269. 4434. 0. 4139. 4018. 3915.]]
The simulator cannot solve Hein 1 from Politiken 1942. Hein puzzles available here.
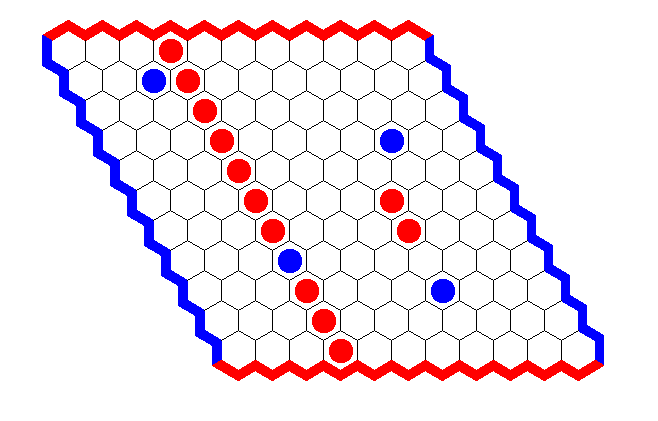
Given board position:
[[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 2. 2. 2. 2. 2. 2. 2. 1. 2. 2. 2.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 2. 2. 0. 1. 0. 0.]
[ 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]]
Simulating 11x11 with N=10000 trials using bernoulli sampling
The P(win|x=1) maximizer:[2, 7, 3176.0]
[[ 2226. 2095. 2210. 2169. 2216. 2239. 2230. 2265. 2454. 2480. 2445.]
[ 2245. 2219. 2130. 2200. 2244. 2187. 2246. 2445. 2675. 2474. 2264.]
[ 2257. 0. 2173. 2164. 2266. 2302. 2387. 3176. 2937. 2180. 2245.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 2176. 2137. 2227. 2212. 2308. 2397. 3032. 3072. 2338. 2217. 2210.]
[ 2161. 2216. 2281. 2237. 2386. 2511. 2604. 2399. 2466. 2238. 2293.]
[ 2169. 2222. 2321. 2297. 2397. 2449. 2241. 2436. 2310. 2234. 2126.]
[ 2212. 2278. 2198. 2376. 2505. 0. 0. 2345. 0. 2233. 2194.]
[ 2223. 2179. 2331. 0. 2262. 2257. 2259. 2302. 2303. 2271. 2182.]
[ 2232. 2302. 2351. 2297. 2372. 2271. 2237. 2211. 2306. 2295. 2216.]
[ 2316. 2303. 2236. 2288. 2226. 2236. 2207. 2276. 2266. 2251. 2230.]]
See Jack's paper: Search and Evaluation in Hex
Sample RP(x) for small boards. (How big is feasible?)
Examine the "gradient ascent" for RP(x)
Suppose x and y are neighbours.
Q. Is it possible that P(x) = P(y)?
Q. If x is a winning opening and P(x) < P(y) then is y also a winning opening?
Suppose x, y, and z are neighbours.
Q. Do we always get a better "pair of neighbours"?
Can P(x) gradient ascent have periodic points?
What "should" the P(x) flow lines look like?
If x_0 is a winning opening and x_n is its forward orbit under P(x)-ascent
then do we get x_n is a winning opening?
The Role of Central Symmetry P(x) = P(-x)
It is often handy to add numbers.
For example, 2+2=4.
"Given examples of x such that P(x) and examples such that not P(x), what is P?"
The puzzle above is the proto-type for all Bongard type puzzles. I'm a fancier of these kind of puzzles, because I think that they really get at an important skill that doesn't get practiced much: inductive thinking. One has to dream up a solution to the problems, there is no formal method for attacking them.
The original canon of Bongard's own Bongard problems and some additional problems, copied from the appendix in Harry Foundalis' thesis, are available without solutions here.
There is also an easy to print edition with six problems per page available: here.
For more information see:
Wikipedia for historical information about Bongard problems.
Linhares, A. (2000). A glimpse at the metaphysics of Bongard problems. Artificial Intelligence, Volume 121, Issue 1-2, pp. 251–270. Available here (mirror). This is a nice paper. It uses the concrete, printed on the page, sense of certain well chosen Bongard problems to talk about metaphysics. It reminds me of the good in Hofstader.
This is a working note about Jürgen Schmidhuber's notion of low-complexity art (wp).
Consider a piece of music, or a text, and call it X. Now -- Fix a programming language, and call it P. We say that the complexity of X relative to P is the length of the shortest program written in P that outputs X. We will call the length of that program K(X,P). This notion is called the Kolmogorov complexity of X measured relative to the programming language P.
It is interesting to note that the language P is irrelevant to definition of K(X,P). Suppose that you wanted work in some other language Q. Now you want to evaluate K(X,Q). Suppose it is possible to implement a Q compiler in P using at most N characters. Over all strings X we know that K(X,Q) is at most K(X,P) + N. Therefore, switching languages only costs a fixed amount of length. And so, we can really ingore the language we work in and think of K(X) in terms of one idealized language.
Kolmogorov complexity expresses a really fundamental idea about information. For example, K(X,P) is not computable. Proof?
Speed Prior (wp) is a nice alternative to K(X,P) since Speed Prior is computable.
"Given a message, what does it mean?"