Just intonation: the harmonic series

Last time I wrote about just intonation, I gave some vague reasons one might want to write music in just intonation. I want to clarify some of that by looking at how exactly intervals work in just intonation. But, in order to do that, it helps to understand the nature of musical pitches, so today, I’m going to cover the harmonic series.

All pitches are made up of sine waves. Unless a pitch is just a single, pure sine wave, it will actually be made up of a whole set of sine waves. The lowest and loudest of these is called the fundamental freqency; when we talk about a 100 Hz pitch, we mean that its fundamental frequency is 100 Hz. The same pitch will also include, at generally decreasing volumes, a 200 Hz frequency, a 300 Hz frequency, 400 Hz, 500 Hz, and so on. The sequence always follows this pattern of n × 1, n × 2, n × 3…

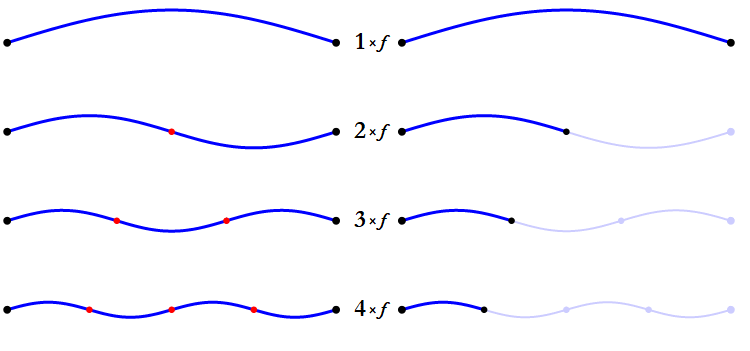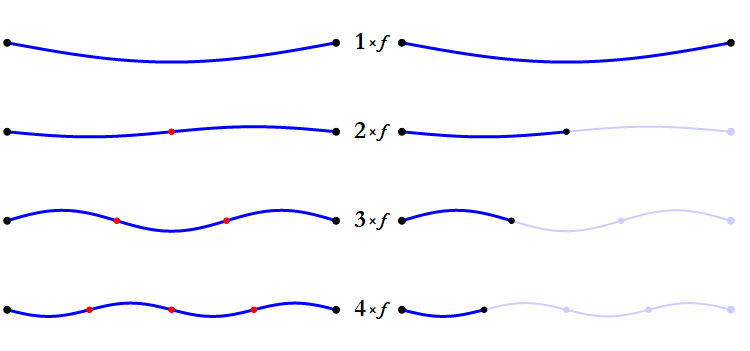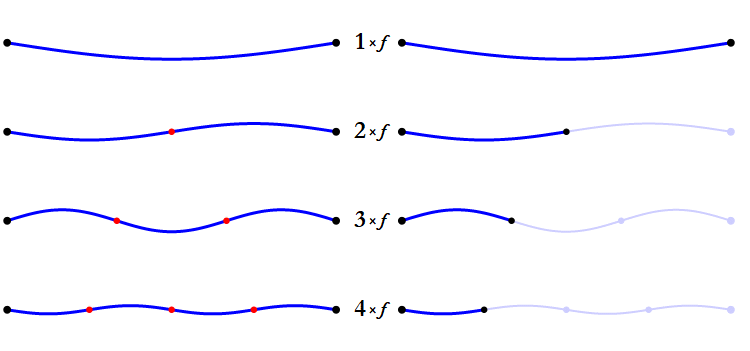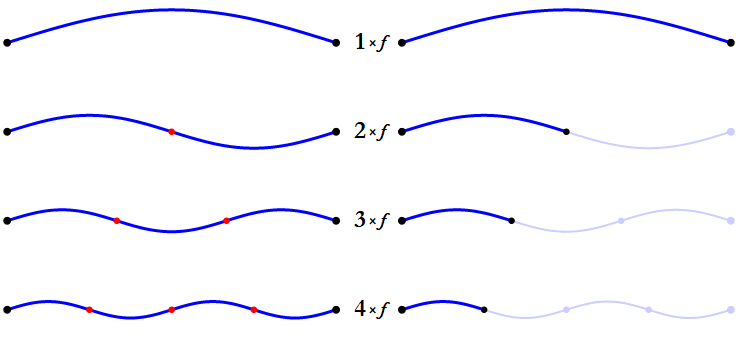
This series of frequencies is called the harmonic series. The existence of this series implies something rather interesting: different musical pitches can share some of their sine waves with each other by means of this series. Here’s a table comparing the beginning of the series for 100 Hz and 200 Hz. Frequencies that 100 Hz shares with 200 Hz are bolded.

This pattern continues, so every other frequency in the 100 Hz series will match a frequency in the 200 Hz series. When two pitches share frequencies like this, they tend to sound aligned with one another. This is generally what we mean when we describe two pitches as “harmonizing” with each other.

In the case above, where one frequency is double the other, the two pitches are as aligned as they can be without literally being the same pitch. Because of this, we tend to perceive notes with this relationship (a doubling of frequency, also known as an octave) as being equivalent in some way. This is known as octave equivalency, and it’s the reason musical notes repeat when you go up a scale and reach the octave.

The next step to take is to look at the intervals produced by multiplying by integers greater than two. From there, we’ll be able to put together a better picture of what you can really do with just intonation.

Have you heard of the harmonic series before from its applications in mathematics? Do notes an octave apart sound similar or equivalent to you? Would you like to hear more about just intonation? Let me know your thoughts at my Ctrl-C email: gome ​@ ​ctrl-c.club.

Next post in series